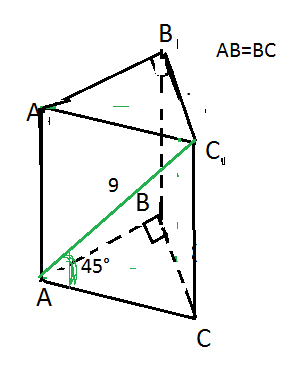
1) Из прямоугольного треугольника АС₁С, острый угол 45°, значит треугольник прямоугольный равнобедренный:
АС=СС₁=9√2/2=4,5√2
H=CC₁=4,5√2
Треугольник АВС - равнобедренный, прямоугольный.
АВ=ВС=4,5
V=S(осн)·H=1/2 AB·BC·H=729√2/8 куб. ед
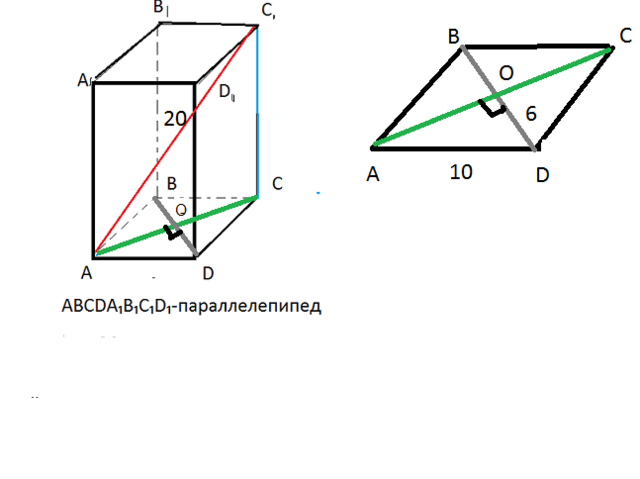
2) В основании ромб ( см. рис.) Р=4a ⇒ 4a=40 ⇒ a=10
Диагонали ромба взаимно перпендикулярны и в точке пересечения делятся пополам.
Рассмотрим прямоугольный треугольник АОD
По теореме Пифагора АО²= AD²-DO²=10²-6²=100-36=64=8²
Значит, АС= 16 см - это бОльшая диагональ, а BD=12 см - мЕньшая
Из треугольника АСС₁ по теореме Пифагора:
СС₁²=АС₁²-АС²=20²-16²=(20-16)(20+16)=4·36=144=12²
CC₁=12
V=S(осн)·H= (1/2) AC·BD·CC₁=(1/2)·12·16·12=1152 куб. см
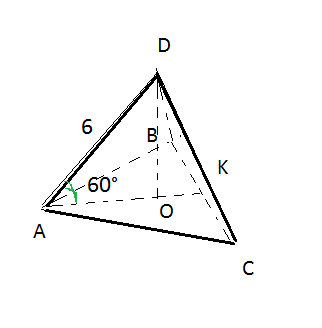
3) Пирамида правильная, в основании равносторонний треугольник.
Проекция вершины D - точка О (центр вписанной окружности)
Из прямоугольного треугольника ADO:
Против угла в 30 градусов лежит катет, равный половине гипотенузы
АО=3 см АО=R=3 cм
ВО²=АВ²-АО²=6²-3²=27
ВО=3√3 см
H=BO=3√3 cм
Площадь равностороннего треугольника равна


 куб. см
куб. см