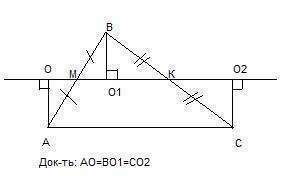
Строим перпендикуляры АО, ВО1, СО2 от вершин к средней линии треуг-ка МК. Нужно доказать, что АО=ВО1=СО2.
Рассмотрим треуг-ки ВКО1 и СКО2. Они равны по стороне и двум прилежащим к ней углам (второй признак равенства треугольников):
- ВК=СК, т.к. МК - средняя линия АВС;
- - У равных треугольников ВКО1 и СКО2 равны соответственные стороны ВО1 и СО2.
Рассмотрим треугольники ВМО1 и АМО. Они также равны по второму признаку равенства треуг-ов:
- АМ=ВМ, т.к. МК - средняя линия АВС;
- - У равных треугольников ВМО1 и АМО равны соответственные стороны АО и ВО1.
Т.к. ВО1=СО2, а АО=ВО1, то АО=ВО1=СО2.