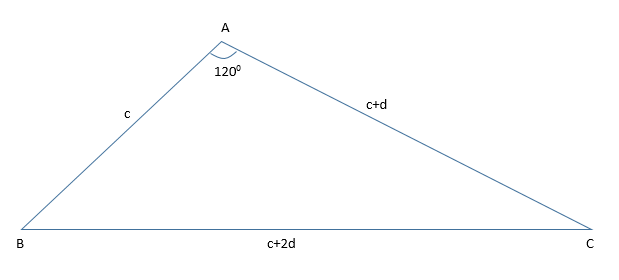
Если стороны образуют арифметическую прогрессию, то их длины:
c
b=c+d
a=b+d=c+2d
Угол в 120° является наибольшим. Поэтому напротив него лежит наибольшая сторона.
Воспользуемся теоремой косинусов:
a²=b²+c²-2bc cos120°
(c+2d)²=(c+d)²+c²-2(c+d)c*(-0.5)
c²+4cd+4d²=c²+2cd+d²+c²+c²+cd
4cd+4d²=3cd+d²+2c²
3d²+cd-2c²=0
Решаем получившееся квадратное уравнение относительно d:
D=c²-4*3(-2c²)=c²+24c²=25c²
√D=5c
d=(-c+5c)/(2*3)=2c/3
(Отрицательные значения корня не рассматриваем, исходя из геометрического смысла)
Следовательно, длины сторон:
с
b=c+2c/3=5c/3
a=c+2*2c/3=7c/3
Тогда искомое отношение сторон
с:b:a=c:5c/3:7c/3=3:5:7
Ответ: 3:5:7