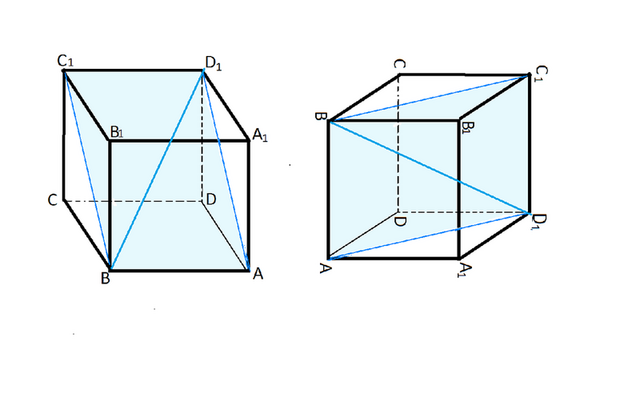
Сечение куба проходит по двум параллельным ребрам оснований и двум диагоналям параллельных граней. Т.е. это прямоугольник АВС₁D₁.
Так как грани куба - квадраты, их диагонали равны длине стороны квадрата, умноженной на √2.
Обозначив длину ребра куба а, получим:
d=ВС₁=АD₁=a√2
Тогда
S☐= а*а√2=25√2
а=√25=5 см
Диагональ куба находят по формуле
D=а√3
Отсюда D=5√3.
-----------------
Так как диагональ куба лежит в плоскости его диагонального сечения, она совпадает с диагональю сечения, которое дано в условии.
Поэтому можно найти диагональ куба и как диагональ этого сечения по т. Пифагора с тем же результатом.