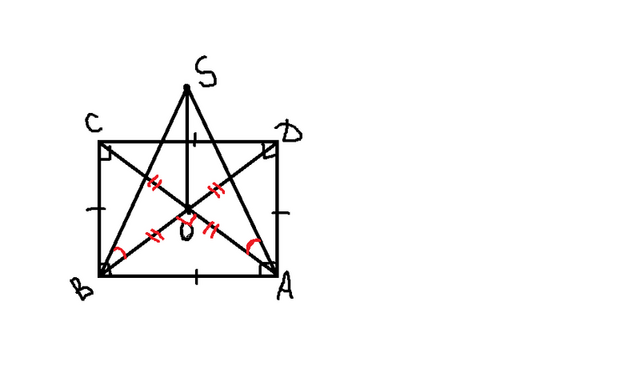
1) стороны квадрата = 11 см, так как периметр это сумма всех сторон , а стороны равны ( 44/4=11см)
2) найдем диагональ квадрата по т.Пифагора
11²+11²=х²
х=√262 см, диагонали точкой пересечения делятся пополам , значит ОА=ОВ=ОС=ОД= √262/2
3) докажем что треугольники АОS= ВОS так как они прямоугольные то по двум признакам
а) ОS- общая сторона
б) ОВ=ОА=√262/2
следовательно треугольники равны по двум катетам, а из равенства треугольников следует равенство углов , значит угол SAO= SBO
ч.т.д