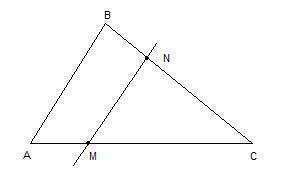
Рассмотрим треугольники АВС и MNC. Они подобны по второму признаку подобия: две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны:
- CN : CB = CM : CA = 9 : 12 = 12 : 16 = 3 : 4 (коэф. подобия 3/4);
- угол С - общий для треугольников.
У подобных треугольников соответственные углы ВАС и NMC равны. Они являются также соответственными углами при пересечении двух прямых АВ и MN секущей АС. Используем один из признаков параллельности двух прямых: если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. Значит, AB II MN.