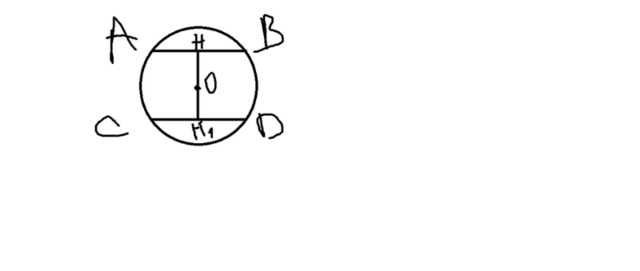Недочет в условии: середины двух ПАРАЛЛЕЛЬНЫХ хорд.
перпендикуляр, опущенный на первую хорду делит ее пополам(то есть является серединным перпендикуляром к хорде). если опустить из центра окружности на другую хорду перпендикуляр, результат тот же получим. получается, что из одной точки проведены два перпендикуляра к параллельным прямым. докажем, что они совпадают(прямые, содержащие перпендикуляры, совпадают - имеется в виду). если из точки опущен перпендикуляр на одну из параллельных прямых, то он будет являться перпендикуляром и к другой прямой >> перпендикуляры совпадают >> прямая, содержащая середины двух параллельных хорд окружности, проходит через центр окружности, что и требовалось доказать.