O₁O₂ = ||O₁K+KO₂|| = r₁+r₂
* * * окружности W₁(O₁;r₁) и W₂(O₂;r₂) касаются внешним образом * * *
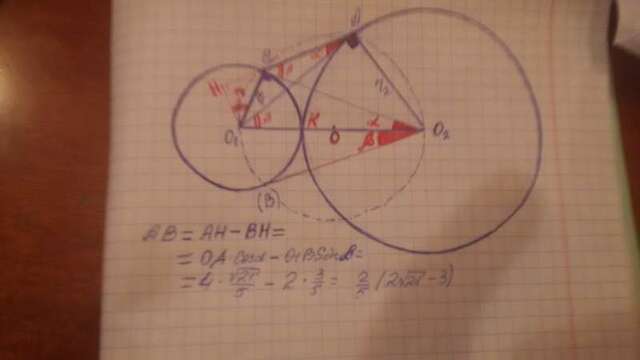
O₂A ⊥ O₁A ;
O₁B ⊥ O₂B
а) док-ть ∠O₁AB = ∠O₁O₂B .
---
б) r₁ =2 , r₂= 3
S(O₁O₂AB) - ?
* * * * * * * * * * * * * *
а) Около любого треугольника можно описать окружность (единственная).
Треугольники O₂AO₁ и O₁BO₂ прямоугольные , поэтому центром описанной около этих треугольников является середина гипотенузы
O₁O₂_ точка O : O₁O =OO₂. Ясно что эти окружности совпадают.
∠O₁AB = ∠O₁O₂B = ◡ O₁nB / 2
( как вписанные углы опирающийся на дугу O₁nB) .
---------------------
б)Для краткости обозначаем ∠O₁AB = ∠O₁O₂B = α ;∠O₂BA=O₂O₁A =∠HO₁B =β
AB =x.
S(O₁O₂AB) =S(O₁O₂A) +S(AO₁B) =(1/2)*AO₁*AO₂ + (1/2)*AO₁*AB*sinα ;
S(O₁O₂AB) = (1/2)*AO₁*(AO₂ +AB*sinα).
AO₁ =√(O₁O₂² - O₂A²) =√( ( r₁+r₂)² - r₂²) = √( (2+3)² -3²) =√( 5² -3²) = 4 .
* * *O₁AO₂ - Пифагорова ∆ , стороны:3,4,5_ натуральные числа * * *
sinα =OB₁ / O₁O₂ =r₁/ r₁+r₂ =2/5 ; cosα =√(1 -sin² α) =√(1 -(2/5)² ) ) =(√21) /5.
Из ΔO₁AB по теореме Пифагора :
O₁B² = AB² +AO₁² -2*AB*AO₁*cosα⇔2² = x² + 4² - 2x*4*(√21) /5 ⇔
5x² - 8√21*x +60 =0 ; D/4 =(4√21) ² - 5*60 =16*21 -300 =336 -300 =36=6²
x₁ = (4√21 +6)/5 >4 не удовлетворяет (AB < AO₁ т.к. ∠O₁BA >90°)
x₂=(4√21 -6)/5 ⇔AB =(4√21 -6)/5 .
S(O₁O₂AB) = (1/2)*AO₁*(AO₂ +AB*sinα)=(1/2)*4*(3 +(4√21-6)/5*(2/5 ))=
=2(3 +(4√21-6)/5* 2/5 ) =2(63+4√21) /25 .
ответ : 2(63+4√21) /25 .