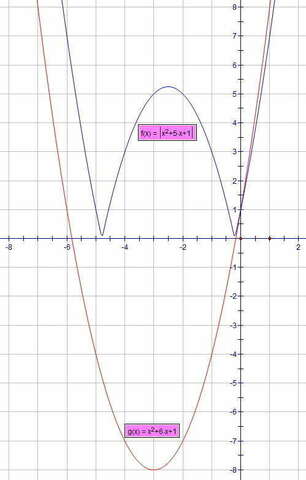
Самое очевидное решение --графическое)))
для x²+5x+1: D=25-4 = 21; (x1;2) = (-5±√21) / 2
для x²+6x+1: D=36-4 = 32; (x1;2) = (-6±√32) / 2 = -3±2√2
в неравенстве знак "меньше", т.е. вопрос неравенства:
на каком промежутке график с модулем "ниже"... сравнив корни:
(-5-√21)/2 ≈ -4.5
-3-2√2 ≈ -5.8 можно сделать вывод: решение возможно только правее корня -3+2√2 для параболы x²+6x+1, т.к. модуль--число неотрицательное не может быть меньше отрицательных значений этой функции (параболы), которые она принимает "между корнями"...
итак, точно: х ≥ -3+2√2 (≈-0.2)
нужно сравнить два правых корня этих парабол (узнать какой из них расположен правее): (-5+√21)/2 или (-3+2√2)
только числитель: -5+√21 или -6+4√2
√21 или -1+√32
чтобы понять что больше, нужно возвести числа в квадрат...
21 или 33-2√32 ?
0 или 12-2√32 ?
0 или √144 - √128 ?
очевидно, что справа число больше, т.е. (-5+√21)/2 < (-3+2√2),
следовательно, модуль раскроется уже со знаком "+" и
осталось решить неравенство
x²+5x+1 < x²+6x+1
5x < 6x
x > 0
это и есть решение...