1) х-3≠0 и х+2≠0;
х≠3 и х≠-2.
Ответ: В) -2 и 3.
2) у=1²+2=1+2=3.
Ответ: А(1;3).
3) х=0:
у=0²-2*0+3=3.
Ответ: В) (0;3).
4) А и В - квадратичные, Б - обратная пропорциональность, Г - линейная.
Ответ: Г) у=2х+3.
5) у=кх-5, точка (3;4).
Выражаем к:
кх=у+5;
к=(у+5)/х;
к=(4+5)/3=9/3=3.
Ответ: Б) к=3.
6) Графики А, Б и В проходят выше оси ОХ, график Г пересекает ось ОХ (у=0):
А) х²+4=0;
х²=-4
Нет решений.
Б) |x|+1=0;
|x|=-1.
Нет решений.
В) 7≠0.
Г) 7х-1=0;
7х=1;
х=1/7.
Ответ: Г) у=7х-1.
7) Найдем точку пересечения графика с осью ОХ, при этом у=0:
2х+8=0;
2х=-8;
х=-4.
Точка (-4;0), значит длина отрезка равна |-4|=4.
Ответ: 4.
8) Так как графики пересекаются, значит их координаты точки пересечения равны, поэтому приравниваем значения у:
х²+2=6;
х²=6-2;
х²=4;
|x|=2;
x=-2 или х=2.
у=6.
(-2;6), (2;6).
Ответ: (-2;6), (2;6).
9. Уравнение прямой у=кх+b, (33 1/3; 99).
Графики линейных функций параллельные, если их коэффициенты пропорциональности к равны, значит к=2.
Уравнение параллельной прямой имеет вид: у=2х+b.
Находим значение b, подставив координаты точки:
b=y-2x=99-2*100/3=99-200/3=97/3=32  .
.
Таким образом, уравнение параллельной прямой
у= 2х+32  .
.
Ответ: y=2x+32 .
.
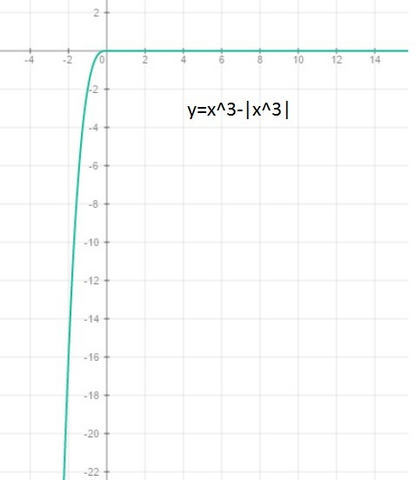
10) График можно построить по точкам:
х -3 -2 -1 0 1 2 3 4
у -54 -16 -2 0 0 0 0 0
График см. на рисунке.