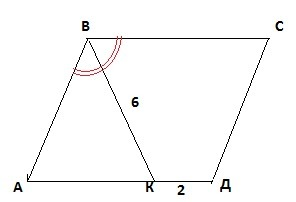
∠АВК=∠КВС=60° (по условию), значит ∠В=120°.
В параллелограмме сумма углов, прилежащих к одной стороне =180°,
поэтому ∠А=180-∠В=180-120=60°⇒ΔАВК-равносторонний,
АВ=АК=ВК=6см⇒ АД=АК+КД=6+2=8.
По свойству параллелограмма СД=АВ=6см, ВС=АД=8см⇒
Р ВСДК=ВК+КД+ВС+СД=6+2+8+6=22см
Ответ: Р=22см