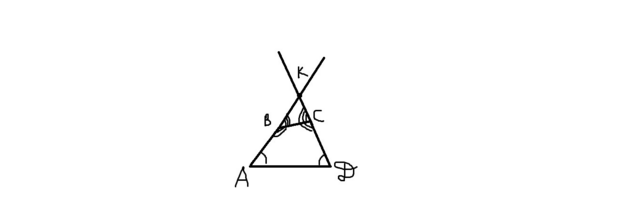
1). Достроим прямые AB и CD до точки их пересечения. Они однозначно пересекутся, т.к. не являются параллельными по условию. Пусть они пересекутся в точке K;
2). Рассмотрим получившийся треугольник AKD. ∠A=∠D, по условию, а значит рассматриваемый треугольник равнобедренный. Т.к. он равнобедренный, из этого следует равенство сторон: AK=DK;
3). Т.к. ∠ABC=∠DCB, по условию, то углы, смежные им, также равны => ∠KBC=∠KCB. Рассмотрим треугольник KBC. Т.к. ∠KBC=∠KCB, то рассматриваемый треугольник равнобедренный. Из этого следует равенство сторон: KB=KC;
4). Теперь объединим получившиеся равенства сторон:
AK=DK из пункта 2;
KB=KC из пункта 3;
AK=AB+KB;
DK=CD+KC;
Т.к. KB=KC, то получаем, что для равенства AK=DK необходимо, чтобы AB=CD, что и требовалось доказать.