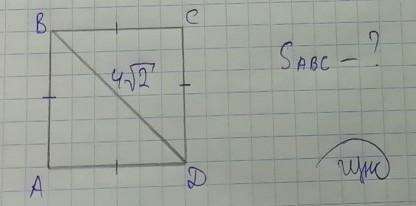
Рассмотрим ΔBCD - прямоугольный (квадрат - это прямоугольник, у которого все стороны равны)
Пусть BC = CD = x. Получим уравнение
BD² = x² + x² (теорема Пифагора)
2x² = (4√2)²
2x² = 32
x² = 32/2 = 16
x = √16 = 4
Площадь квадрата равна квадрату его стороны
S = a²
S = 4² = 16 ед.
Ответ: S = 16 ед.