Ответ:
а) n=6. б) точка В лежит между точками А и С.
в) точка В делит отрезок АС пополам.
Объяснение:
а) чтобы точка С(-2;n) лежала на прямой АВ, уравнение которой :
4x+3y-10 = 0, необходимо, чтобы координаты этой точки удовлетворяли уравнению прямой АВ. То есть, подставив координаты точки С в уравнение, мы должны получить равенство.
4*(-2) +3*n - 10 = 0. 3n = 18. n = 6.
Ответ: n = 6.
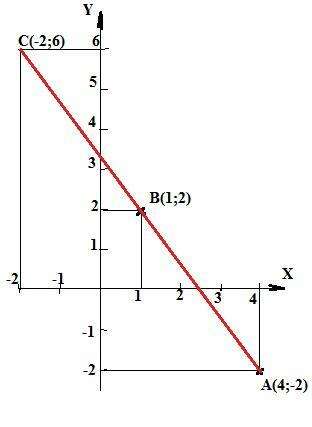
б). Точка В(1;2) лежит между точками А(4;-2) и C(-2;6) , так как координаты точки лежат между соответствующими координатами этих точек: для х: -2 < 1 <4, для y: 6 > 2 > -2.
в) Длина отрезка АС (модуль вектора АС):
|AC| = √((Xc-Xa)²+(Yc-Ya)²) = √((-6)²+ 8²) = 10 ед.
Длины отрезков АВ и ВС:
|AB| = √((Xb-Xa)²+(Yb-Ya)²) = √((-3)²+4²) = 5 ед.
|BC| = √((Xc-Xb)²+(Yc-Yb)²) = √(-3)²+4²) = 5 ед.
Ответ: точка В делит отрезок АС пополам, то есть АВ/ВС=1/1.
P.S. Рисунок для иллюстрации.