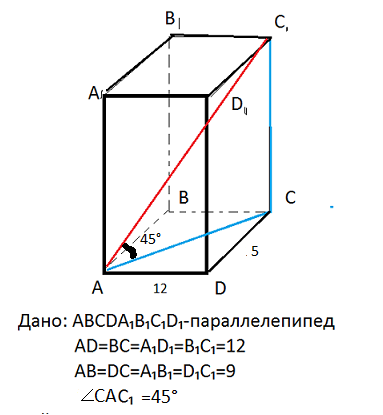
Теория- прямоугольные треугольники. В основании прямоугольник. Диагональ АС делит его на два прямоугольных треугольника
По теореме Пифагора
АС²=AD²+DC²=12²+5²=144+25=169=13²
АС=13
Треугольник АСС₁ - прямоугольный. Ребро СС₁ ⊥ плоскости основания ABCD, а значит перпендикулярно любой прямой, лежащей в плоскости
Угол между диагональю АС₁ и плоскостью основания - угол между диагональю АС₁ и её проекцией на плоскость АВСD. А проекцией будет диагональ АС.
Значит в прямоугольном треугольнике АСС₁ острый угол 45°, второй острый угол тоже 45°. Сумма острых углов прямоугольного треугольника 90°
Треугольник АСС₁ - прямоугольный равнобедренный, АС=СС₁=13