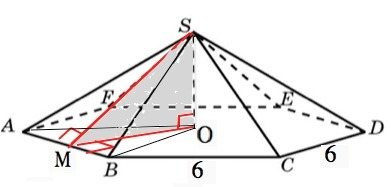
Основание правильной пирамиды - правильный многоугольник, а её вершина проецируется в центр многоугольника.
Для правильной шестиугольной пирамиды центр основания - точка пересечения её диагоналей.
Формула объёма пирамиды V=S•H:3
В основании данной пирамиды правильный шестиугольник, площадь которого равна площади 6-ти равносторонних треугольников.
Формула площади ∆ (АОВ)=a²√3/4.
SM=AB=6 см
S(основания)=6•S(AOB)=6•36√3/4=54√3 см²
Высоту ЅО найдем по т.Пифагора из прямоугольного ∆ SOM.
SO=√(SM²-OM²)
ОМ=ОВ•sin60°=6√3/2=3√3⇒
ЅО=√(36-27)=3 см
V=(54√3)•3:3=54√3 см³