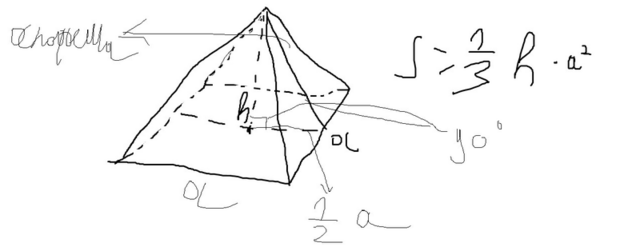
Объем пирамиды по формуле v=1/3h a^2
где h высота a - это сторона квадрата в основании
тогда у нас есть прямоугольный треугольник из апофемы и бокового ребра
а недостающий катет это 1/2 стороны квадрата основания, воота
тогда 1/2 стороны равна по теореме Пифагора x=sqrt(10^2-8^2) и равна 6
дальше поскольку это половина стороны мы умножаем её на 2 и того сторона квадрата основания равна 12
дальше нам не хватает высоты, её мы тоже находим через теорему Пифагора там получается второй прямоугольный треугольник с гипотенузой - апофемой, первый катет это 1/2 стороны квадрата - 6
второй наш искомый
x=sqrt(8^2-6^2)=корень из 28
тогда по первой формуле получается ответ 96корень из 7
ps сомневаюсь что это правильно но я пытался ((9(