1) Угол между касательными, проведенными из одной точки, равен 180 минус величина меньшей заключенной внутри него дуги.
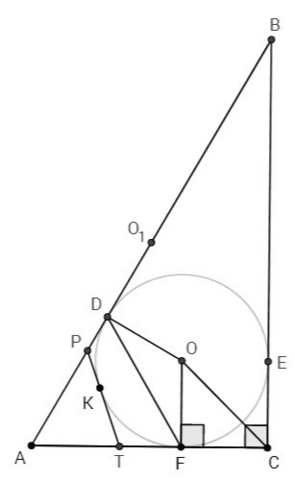
Д-во: Рассмотрим четырехугольник, образованный отрезками касательных и радиусами (ADOF). Сумма углов четырехугольника 360. Углы между касательными и радиусами 90 (ADO, AFO). Угол между отрезками касательных (DAF) равен 180 минус угол между радиусами (DOF). Центральный угол (DOF) равен величине дуги, которую он стягивает (U DF).
∠DOE=180-∠DOE=180-30=150
∠FOE=180-90=90
∠DOF=180-∠DAF=180-60=120
150:90:120 = 5:3:4
2) Центр вписанной окружности лежит на биссектрисе, ∠OCF=90/2=45, ∠CFO=90 (угол между касательной и радиусом), ∠FOC=180-90-45=45
△FOC - равнобедренный => OF=FC
По теореме Пифагора:
OF^2+FC^2=OC^2 <=> 2OF^2=32 <=> OF=4
3) Теорема косинусов (△DOF):
DF^2=DO^2+OF^2-2*DO*OF*cos(DOF) <=> DF=√(2*16*1,5)=4√3
AD=AF (отрезки касательных, проведенных из одной точки, равны)
△FAD - равнобедренный, ∠A=60 => △FAD - равносторонний => AD=AF=DF
PK=PD, TK=TF (отрезки касательных, проведенных из одной точки, равны)
P APT = AP+PK+AT+TK = AP+PD+AT+TF = AD+AF = 2DF = 8√3
4) В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы. Медиана, проведенная из прямого угла, равна половине гипотенузы => △AO1C - равнобедренный, ∠A=60 => △AO1C - равносторонний => AO1=AC
R= AO1 = AF+FC = 4√3+4 (~10,93)