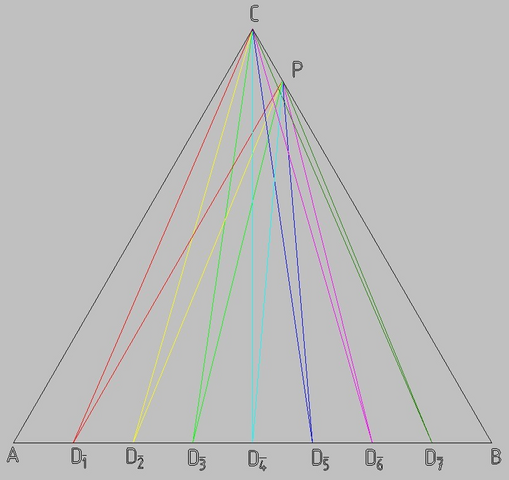
Их тут 7, а не 6, как вчера :)
∠CD₁P = ∠CD₁B-∠PD₁B, аналогично для всех остальных
S = ∠CD₁P+∠CD₂P+∠CD₃P+∠CD₄P+∠CD₅P+∠CD₆P+∠CD₇P =
∠CD₁B+∠CD₂B+∠CD₃B+∠CD₄B+∠CD₅B+∠CD₆B+∠CD₇B -
(∠PD₁B+∠PD₂B+∠PD₃B+∠PD₄B+∠PD₅B+∠PD₆B+∠PD₇B)
Жуть. Но, какое везение, многие углы здесь дают в сумме 180 градусов, объединяясь в пары - как угол при основании равнобедренного треугольника икак внешний угол с другой стороны основания этого же равнобедренного треугольника
∠CD₁B+∠CD₇B = 180°
∠CD₂B+∠CD₆B = 180°
∠CD₃B+∠CD₅B = 180°
∠CD₄B = 90°
∠PD₁B = 60°
∠PD₂B+∠PD₇B = 180°
∠PD₃B+∠PD₆B = 180°
∠PD₄B+∠PD₅B = 180°
Итого
S = 180°*3+90° - 60°-3*180° = 90°-60° = 30°