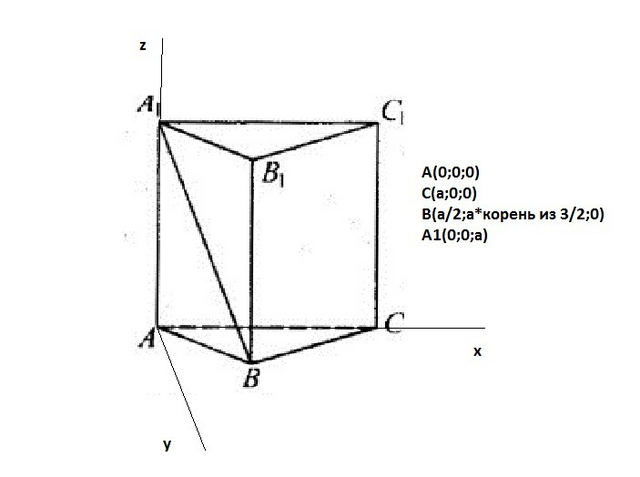
1а) CC1||BB1, поэтому угол найду между А1В и ВВ1
ΔА1В1В-прямоугольный и равнобедренный, поэтому искомый угол 45
1б) между скрещивающимися прямыми удобнее находить угол, используя метод координат
ВА1=(-a/2;-a*√3/2;a); AC=(a;0;0)
|BA1|=a√2; |AC|=a
распишу скалярное произведение этих векторов в координатах и через угол
-a^2/2=a^2*√2*cosx; cosx=-1/√2
так как cosx не равен 0, значит угол между прямыми ВА1 и АС не прямой
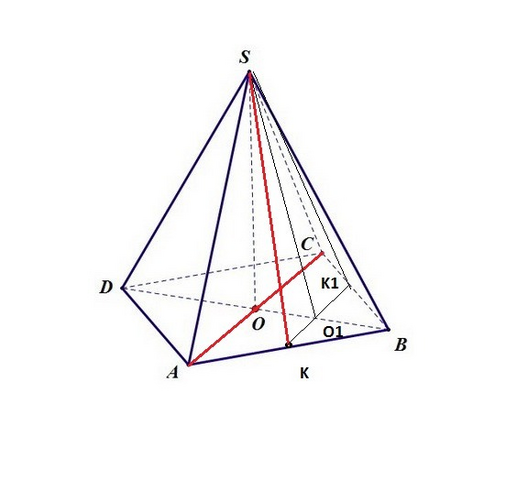
2)Искомый угол равен углу SKK1 в равнобедренном ΔSKK1
KK1=AC/2=a/√2
SK=SK1 из равнобедренного ΔАВS высота SK^2=a^2-(a/2)^3=3a^2/4; SK=a*√3/2
из прямоугольного ΔSKO1 найду cosK=KO1/KS=KK1/(2KS)=(a/√2)/(2*a*√3/2)=1/√6
Угол между SK и АС примерно 66 градусов